Aprender fracciones es fundamental en matemáticas porque nos permite comprender cómo se dividen y relacionan las partes de un todo. Además, aportan una lógica que es clave para entender proporciones, y sus contenidos funcionan como base de muchos otros temas de matemática.
Por todo esto, su dominio es fundamental, no solo para resolver problemas académicos y tener un buen desempeño en los diferentes niveles de la educación, sino también para aplicar en una amplia variedad de situaciones de la vida cotidiana como repartir, medir o comparar cantidades.
A continuación, exploraremos en profundidad los diferentes tipos de fracciones que existen poniendo especial atención en las fracciones propias e impropias y mixtas, sus características principales y las diferencias que presentan entre sí.
¿Qué son las fracciones?
Una fracción es un concepto matemático que se utiliza para representar una cantidad que no es un número entero, y que expresa cómo se divide un total en partes iguales. Se escribe con números separados por una línea:
El número que se escribe arriba de la línea se llama numerador y señala cuántas partes se toman del total.
El número que se escribe debajo de la línea se llama denominador y representa la cantidad de partes iguales en que se ha dividido al todo.
👉 Por ejemplo, en la fracción:
El denominador 4 indica que el total está dividido en 6 partes iguales, y el numerador 3, indica que de ese total se toman 3 partes.
Por ejemplo, podemos pensar en la fracción 4/8 a través de una pizza. El denominador 8, nos indica que la pizza fue dividida en 8 porciones, y su numerador, 4, que se tomaron 4 porciones del total (es decir, la mitad).
Esta forma que indica cuántas partes de un total se toman a través de la representación del numerador y del denominador, es el modo más básico de las fracciones. Sin embargo, no todas representan siempre una parte menor que la unidad. Existen diferentes fracciones que hacen referencia a distintos tipos de proporciones o cantidades: algunas son más pequeñas que el entero (propias), otras lo superan (impropias) y, en ciertos casos, pueden expresarse combinando un número entero con una fracción (mixtas). A continuación, veremos en detalle cada uno de estos tipos.
¿Cuáles son las fracciones propias?
Son aquellas en las que el numerador es menor que el denominador. Es decir, siempre representan una cantidad menor que la unidad (1). Ej: 
Las fracciones propias y sus operaciones son las más fáciles. Además, se pueden reconocer rápidamente, ya que el numerador (número de arriba) es menor que el denominador (número de abajo): esta es la principal característica de este tipo de fracciones.
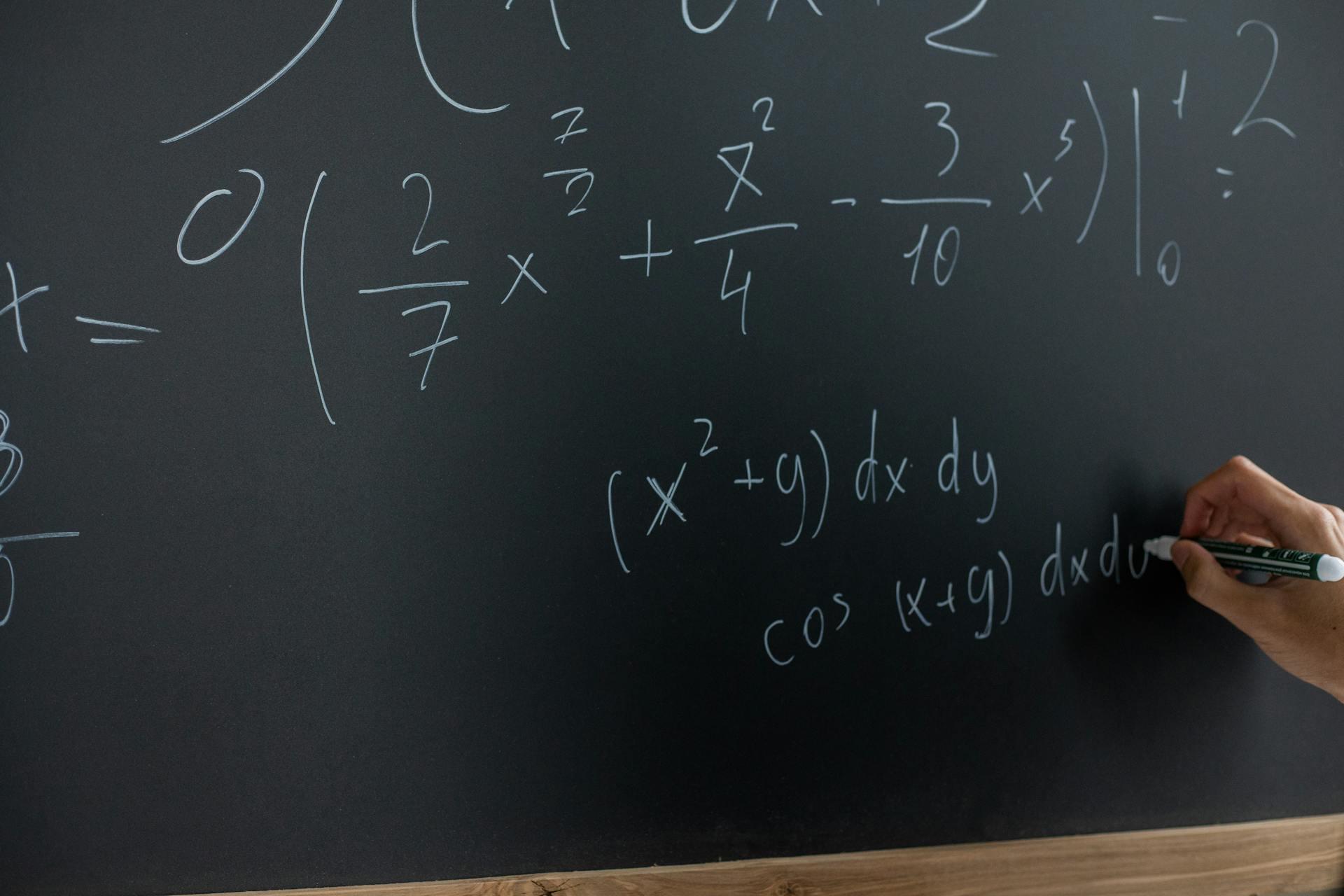
Al tener un numerador menor, las fracciones propias siempre representan una cantidad menor a la unidad (1). ¿Qué quiere decir esto? Significa que nos muestran una parte del todo, o del total, sin llegar a completarlo.
Por tal motivo, en las fracciones propias, si se divide el numerador entre el denominador, el resultado siempre será un número decimal inferior a 1.
👉 Veamos algunos ejemplos:
¡Descubrí qué son las fracciones equivalentes y cómo reconocerlas fácilmente!
¿Cuáles son las fracciones impropias?
Son aquellas en las que el numerador igual o mayor que el denominador. Por eso, representan una cantidad igual o mayor que la unidad (1). Ej:
En las fracciones impropias el numerador (número superior) es más grande o igual que el denominador (número inferior). Esta es la principal característica de este tipo de fracciones.
Esta relación hace que, a diferencia de las fracciones propias, las impropias representen cantidades que son iguales o superiores a la unidad (1). ¿Qué significa esto? Quiere decir que muestran que se han tomado tantas partes del todo como las que lo forman, o incluso más.
Entonces, al dividir el numerador entre el denominador, el resultado es siempre 1 o superior.
👉 Ejemplos:
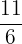
¿Te gustaría aprender cómo es la multiplicación de fracciones?
¿Se puede convertir una fracción impropia a un número entero?
Una fracción impropia se puede transformar en un número entero solo cuando el numerador el un múltiplo exacto del denominador.
Un múltiplo es el resultado que se obtiene al multiplicar un número por un número entero. Dicho de otra manera, un múltiplo es la cantidad que contienen al número original varias veces.
👉 Por ejemplo:
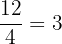
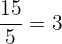
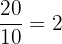
En estos casos, la división se resuelve sin dejar resto, lo que permite obtener directamente un número entero. Es importante prestar atención a este tipo de fracciones, ya que no siempre es posible esta conversión: cuando el numerador no es múltiplo del denominador, el resultado será un número decimal o una fracción mixta.
¿Ya sabés cuáles son los mejores métodos para sumar fracciones?
Fracciones mixtas
Son una combinación de un número entero y una fracción propia. Se utilizan para expresar de manera más clara una fracción impropia. Ej: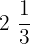
Las fracciones mixtas, también llamadas números mixtos, son expresiones que combinan un número entero con una fracción propia. Se utilizan como una manera alternativa y más clara de representar ciertas fracciones impropias.
Por ejemplo, en lugar de escribir la fracción 7/3 (siete tercios), la misma puede expresarse como 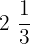lo que significa "dos enteros de un tercio".
👉 Ejemplos:
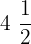
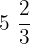
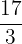
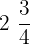
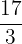
¿Cómo convertir una fracción impropia a una mixta?
Transformar una fracción impropia (numerador mayor que el denominador) a una mixta (combina un número entero y una fracción propia, es bastante sencillo. Para ello, solo tenemos que tomar el numerador de la fracción impropia y dividirlo entre el denominador de la misma.
El cociente de la división será el número entero (de la fracción mixta) y el resto de la división, será el numerador de la fracción propia que queda. La fracción conserva el mismo denominador.
👉 Ejemplo:
9÷4
Cociente: 2/ Resto: 1.
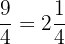
Tener claro los mecanismos de conversión de fracciones es fundamental para poder realizar diferentes operaciones con las mismas.
Por ejemplo, en el caso de la suma de fracciones, resulta práctico unificar su forma antes de operar. Es decir, convertir todas las fracciones intervinientes, ya sea a impropias, propias o mixtas, según convenga. Esto facilita el cálculo porque el procedimiento exige encontrar un denominador común, y trabajar con un mismo tipo de fracción hace que el proceso sea más claro y ordenado.
¿Te gustó este artículo? ¡Puntualo!
Loading...
