Si estás estudiando fracciones y sus operaciones, entender el concepto de fracciones equivalentes es clave. Se trata de un tema que puede parecer complicado, pero que una vez que se lo internaliza y que se comprende su utilidad, se vuelve un gran aliado para razonar fracciones.
Además, se trata de un tema que sienta las bases lógicas para poder aprender otros conceptos de matemáticas, por lo que es esencial estudiarlo e incorporarlo de manera eficiente.
Si ya lo estuviste viendo, pero sentís que es imposible, ¡no te preocupes! A continuación, te explicamos paso a paso que son las fracciones equivalentes, para qué sirven, cómo encontrarlas y cómo operar con ellas. Además, te ofrecemos ejemplos prácticos para que puedas ver cuál es su aplicación y puedas integrar la teoría con la práctica de la mejor manera.
Definición de fracciones equivalentes
Aprender qué son las fracciones equivalentes es mucho de más fácil de lo que su nombre aparenta. Vamos a ver:
Las fracciones equivalentes son aquellas que aunque tienen diferentes números en el numerador y en el denominador, representan la misma cantidad o proporción.
👉 Por ejemplo:
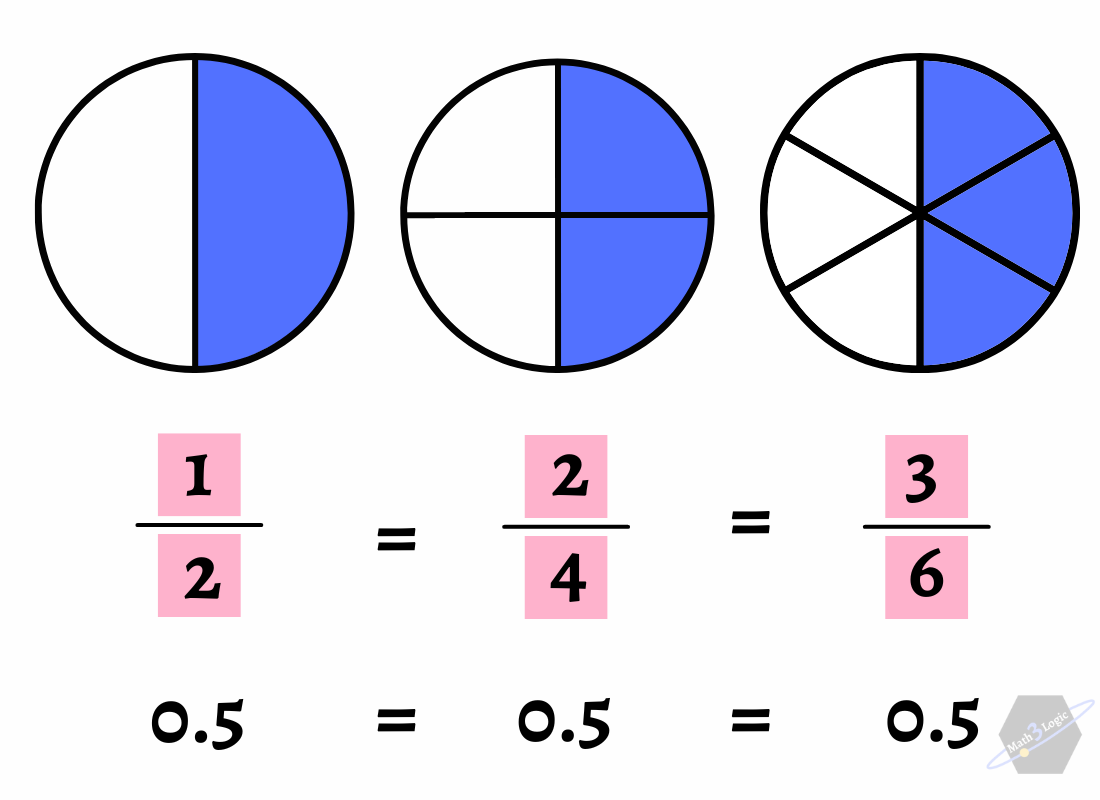
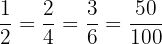
son equivalentes porque simbolizan la mitad.
En la primera imagen, el todo se encuentra dividido en dos secciones iguales y una de ellas aparece pintada, lo que corresponde a la mitad, es decir, a la fracción 1/2.
En la segunda, el mismo espacio se separó en cuatro partes iguales y se colorearon dos, representando también a la mitad, es decir, a la fracción 2/4.
En la tercera figura, el área total se fraccionó en seis segmentos y se marcaron tres, que equivalen a 3/6.
Entonces, si observamos con atención, podremos notar que la zona coloreada es siempre de igual tamaño en las tres imágenes, aunque los números que la simbolizan en la fracción varíen. Eso significa que 1/2, 2/4 y 3/6 expresan la misma cantidad: se trata de fracciones equivalentes.
Todas estas fracciones hacen referencia a la misma cantidad o proporción, más allá de que tengan un numerador y un denominador diferentes.
¿Cómo detectar si dos fracciones son equivalentes?
Existen varios métodos que se utilizan para saber si dos fracciones son equivalentes. Son sencillos y es importante poder dominarlos, ya que nos servirán como herramientas a las que podremos acudir en diferentes momentos y según el tipo de fracciones que se nos presenten.
1. Multiplicación cruzada
La multiplicación cruzada es una de las formas más fáciles y rápidas de comprobar si existe equivalencia entre dos fracciones.
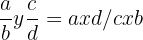
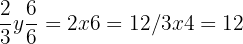
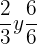
son equivalentes.
¿Ya sabés cuáles son los mejores métodos para sumar fracciones?
2. Simplificación
Simplificar una fracción significa reducirla a su forma más simple. Esto se hace dividiendo el numerador y el denominador por el mismo número (distinto a 0).
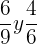
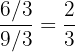
simplificada es 
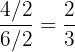
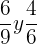
simplificada es son fracciones equivalentes.
3. Valor decimal: dividiendo numerador por denominador
Este método súper sencillo consiste en dividir el numerador por el denominador en ambas fracciones. Si el resultado decimal es igual, significa que las dos fracciones en cuestión representan la misma cantidad.
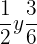
Dividimos el numerador por el denominador de 1/2: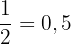
Dividimos el numerador por el denominador de 3/6: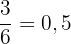
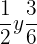
son equivalentes.
4. Amplificación
La amplificación consiste en crear una fracción equivalente a partir de otra. Esto se hace multiplicando el numerador y el denominador por el mismo número.
Es decir, más que una forma de comprobación de equivalencia, la amplificación es una herramienta que se utiliza para construir equivalencias entre fracciones.
la amplificamos multiplicando numerador y denominador por un número igual. En este caso haremos la amplificación x 2.
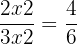
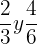
son equivalentes.
¿Te gustaría aprender cómo es la multiplicación de fracciones?
Ejemplos de fracciones equivalentes
A continuación te proponemos una serie de ejemplos que son fracciones equivalentes entre sí. Te proponemos imágenes que representan a las fracciones a fin de que puedas visualizar y comprender claramente por qué son equivalentes.
Ejemplo 1:
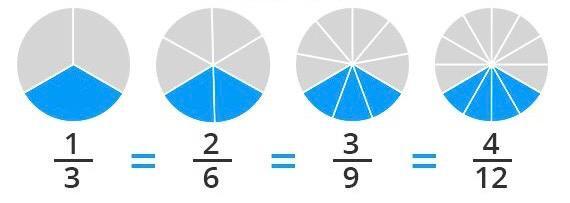
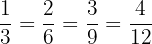
son equivalentes porque simbolizan 1/3.
En la primera imagen, el total se encuentra dividido en tres secciones iguales y una de ellas aparece pintada, lo que corresponde a un tercio, es decir, a la fracción 1/3.
En la segunda, el mismo espacio se dividió en seis partes iguales, y se colorearon dos. Esto también representa un tercio del total, es decir, a la fracción 2/6.
En la tercera figura, el área total se segmentó en nueve partes, de las cuales se colorearon tres, que equivalen a 3/9.
Finalmente, en la cuarta imagen, la figura total se dividió en doce partes iguales y se colorearon 4. Esto corresponde a la fracción 4/12.
👉 Entonces, si observamos con atención, podremos notar que la superficie total y la zona coloreada es siempre de igual tamaño en todas las imágenes, aunque los números que simbolizan cada fracción varíen. Eso significa que 1/3, 2/6, 3/9 y 4/12 expresan la misma cantidad: se trata de fracciones equivalentes, por más de que sus numeradores y denominadores sean diferentes.
Ejemplo 2
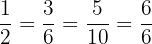
son equivalentes porque hacen referencia a 1/2.
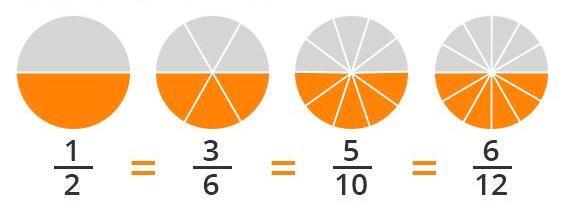
En el primer círculo, el entero está dividido en dos partes iguales y se colorea una. Esto corresponde a la fracción 1/2.
En la segunda figura, el mismo espacio aparece separado en seis secciones y se pintan tres, que equivalen a 3/6.
En la tercera, el área se fraccionó en diez porciones y iguales, de las que se colorearon 5. Esto representa a la fracción 5/10.
Finalmente, en la cuarta, el todo se dividió en doce partes iguales y se colorearon seis, lo que da lugar a la fracción 6/12.
👉 Entonces, al observar todos los círculos juntos, se nota que las partes sombreadas ocupan siempre la misma proporción del todo, aunque los números de la fracción sean distintos. Esto significa que 1/2, 3/6, 5/10 y 6/12 expresan la misma cantidad, es decir, son fracciones equivalentes.
¡Descubrí cuáles son los diferentes tipos de fracciones que existen!
Ejemplo 3
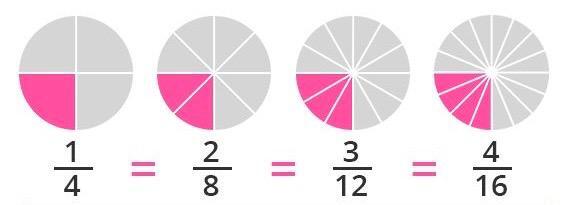
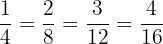
son equivalentes porque hacen referencia a 1/4 del total.
En la primera figura, el todo está dividido en cuatro partes iguales y se coloreó una. Esto corresponde a la fracción 1/4.
En la segunda, el mismo espacio se partió en ocho secciones y se colorearon dos, lo que equivale a 2/8.
En la tercera imagen, el área total aparece dividida en doce porciones y se marcaron tres. Esto corresponde a 3/12.
Por último, en la cuarta figura, el total se separó en dieciséis partes de las cuales se pintaron cuatro. Esto representa la fracción 4/16.
👉 Si miramos todas las figuras en conjunto, notamos que el área sombreada ocupa siempre la misma proporción del todo, aunque cambien los números de la fracción. De esta forma, podemos visualizar que 1/4, 2/8, 3/12 y 4/16, más allá de que tengan diferentes numeradores y denominadores, expresan exactamente la misma cantidad: son fracciones equivalentes.
Como verás, comprender y detectar equivalencias en fracciones, una vez que se tiene el método incorporado es relativamente sencillo, sobre todo en comparación con otros temas como la suma de fracciones. Para seguir aprendiendo de forma personalizada, ¡no dudes en recurrir a uno de nuestros profesores particulares de matemáticas!
¿Te gustó este artículo? ¡Puntualo!
Loading...
